Introduction to Quadratic Functions
What is a Quadratic Function?
Quadratic equations are second order polynomials, and have the form .Learning Objectives
Describe the criteria for, and properties of, quadratic functionsKey Takeaways
Key Points
- A quadratic function is of the form , where a is a nonzero constant, b and c are constants of any value, and x is the independent variable.
- The solutions to a quadratic equation are known as its zeros, or roots.
Key Terms
- dependent variable: Affected by a change in input, i.e. it changes depending on the value of the input.
- independent variable: The input of a function that can be freely varied.
- vertex: The minimum or maximum point of a quadratic function.
- quadratic function: A function of degree two.
Differences Between Quadratics and Linear Functions
Quadratic equations are different than linear functions in a few key ways.- Linear functions either always decrease (if they have negative slope) or always increase (if they have positive slope). All quadratic functions both increase and decrease.
- With a linear function, each input has an individual, unique output (assuming the output is not a constant). With a quadratic function, pairs of unique independent variables will produce the same dependent variable, with only one exception (the vertex ) for a given quadratic function.
- The slope of a quadratic function, unlike the slope of a linear function, is constantly changing.
Forms of Quadratic Functions
Quadratic functions can be expressed in many different forms. The form written above is called standard form. Additionally is known as factored form, where and are the zeros, or roots, of the equation. These are values at which the function crosses the y-axis (and thus where equals zero). The vertex form is displayed as: where and are respectively the coordinates of the vertex, the point at which the function reaches either its maximum (if is negative) or minimum (if is positive).The Quadratic Formula
The zeros of a quadratic equation can be found by solving the quadratic formula.Learning Objectives
Solve for the roots of a quadratic function by using the quadratic formulaKey Takeaways
Key Points
- The quadratic formula is: , where and are the coefficients of the and terms, respectively, in a quadratic equation, and is the value of the equation's constant.
- To use the quadratic formula, must equal zero and must not be zero.
Key Terms
- zero: Also known as a root, an value at which the function of is equal to 0.
Criteria For Use
To use the quadratic formula, two criteria must be satisfied:- The quadratic equation must equal zero;
- must not equal zero
Solving Quadratic Equations with the Quadratic Formula
Solutions to can be found by using the quadratic formula The symbol ± indicates there will be two solutions, one that involves adding the square root of , and the other found by subtracting said square root. The resulting values (zeros) may or may not be distinct, and may or may not be real.Example
Let's take a look at an example. Suppose we want to find the roots of the following quadratic function: First, we need to set the function equal to zero, as the roots are where the function equals zero. Second, we need to identify the constants in the equation. The value of is two, the value of is five, and the value of is three. We can now substitute these values into the quadratic equation and simplify:The Discriminant
The discriminant of a polynomial is a function of its coefficients that reveals information about the polynomial's roots.Learning Objectives
Explain how and why the discriminant can be used to find the number of real roots of a quadratic equationKey Takeaways
Key Points
- is the formula for a quadratic function 's discriminant.
- If Δ is greater than zero, the polynomial has two real, distinct roots.
- If Δ is equal to zero, the polynomial has only one real root.
- If Δ is less than zero, the polynomial has no real roots, only two distinct complex roots.
- A zero is the x value whereat the function crosses the x-axis. That is, it is the x-coordinate at which the function's value equals zero.
Key Terms
- quadratic: Of degree two; can apply to polynomials.
- zero: Also known as a root; an x value at which the function of x is equal to zero.
- discriminant: An expression that gives information about the roots of a polynomial.
The Discriminant and the Quadratic Formula
Recall the quadratic formula: where , and are the constants ( must be non-zero) from a quadratic polynomial. The discriminant is the portion of the quadratic formula under the square root.Positive Discriminant
If is positive, the square root in the quadratic formula is positive, and the solutions do not involve imaginary numbers. Because adding and subtracting a positive number will result in different values, a positive discriminant results in two distinct solutions, and two distinct roots of the quadratic function.Zero Discriminant
If is equal to zero, the square root in the quadratic formula is zero: Since adding zero and subtracting zero in the quadratic equation lead to the same outcome, there is only one distinct root of the quadratic function.Negative Discriminant
If is less than zero, the value under the square root in the quadratic formula is negative: This means the square root itself is an imaginary number, so the roots of the quadratic function are distinct and not real.Example
Consider the quadratic function: Using as the value of , as the value of , and as the value of , the discriminant of this function can be determined as follows: Because Δ is greater than zero, the function has two distinct, real roots. Checking graphically, we can confirm this is true; the zeros of the function can be found at and .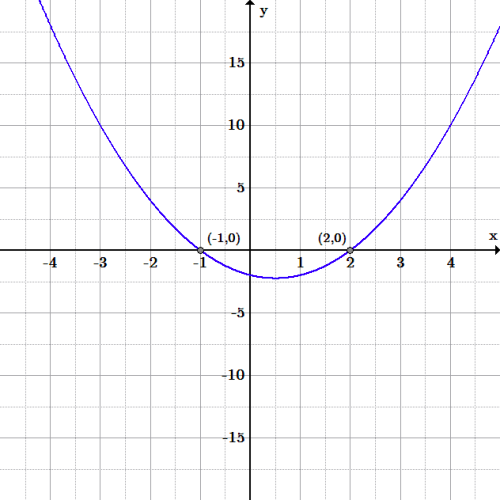 Example: Graph of a polynomial with the quadratic function . Because the value is greater than 0, the function has two distinct, real zeros. The graph of shows that it clearly has two roots: the function crosses the -axis at and .
Example: Graph of a polynomial with the quadratic function . Because the value is greater than 0, the function has two distinct, real zeros. The graph of shows that it clearly has two roots: the function crosses the -axis at and .Other Equations in Quadratic Form
Many equations with no odd-degree terms can be reduced to quadratics and solved with the same methods as quadratics.Learning Objectives
Use the quadratic formula to solve any equation in quadratic formKey Takeaways
Key Points
- A biquadratic equation (quartic equation with no terms of odd- degree ) has the form . It can be expressed as: (where ).
- The values of can be found by graphing, factoring, completing the square, or using the quadratic formula. Their square roots (positive and negative) are the values of that satisfy the original equation.
- Higher-order equations can be solved by a similar process that involves reducing their exponents. The requirement is that there are two terms of such that the ratio of the highest exponent of to the lower is .
Key Terms
- zero: Also known as a root; an value at which the function of is equal to zero.
- biquadratic: When a polynomial involves only the second and fourth powers of a variable.
- quartic function: Any polynomial function whose greatest exponent is of power four.
Example
As an example, consider the equation: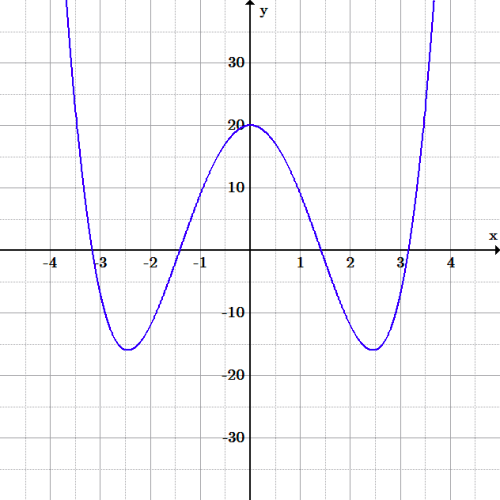 Quartic graph: Graph of the function .
Quartic graph: Graph of the function .We can substitute the arbitrary variable in place of :
This equation is now solvable for using the quadratic formula: Simplifying this, we find equals 2 or 10. Knowing that , we can use each value of to solve for two values of : A similar procedure can be used to solve higher-order equations. The requirement is that there are two terms of such that the ratio of the highest exponent of to the lower is .