Counting and Probability
Introduction
What you'll learn to do: Apply counting formulas to calculate the probability of complex events
Counting? You already know how to count or you wouldn't be taking a college-level math class, right? Well yes, but what we'll really be investigating here are ways of counting efficiently. When we get to the probability situations a bit later in this chapter we will need to count some very large numbers, like the number of possible winning lottery tickets. One way to do this would be to write down every possible set of numbers that might show up on a lottery ticket, but believe me: you don't want to do this.
Learning Outcomes
- Solve counting problems using permutations
- Solve counting problems using combinations
- Compute the probability of events within a complex counting problem
The Basic Counting Rule
We will start with some simple counting problems in order to develop the ideas that we will soon need.example
Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks) and five choices for a main course (hamburger, sandwich, quiche, fajita or pizza). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have? Solution 1: One way to solve this problem would be to systematically list each possible meal: soup + hamburger soup + sandwich soup + quiche soup + fajita soup + pizza salad + hamburger salad + sandwich salad + quiche salad + fajita salad + pizza breadsticks + hamburger breadsticks + sandwich breadsticks + quiche breadsticks + fajita breadsticks + pizza Assuming that we did this systematically and that we neither missed any possibilities nor listed any possibility more than once, the answer would be 15. Thus you could go to the restaurant 15 nights in a row and have a different meal each night. Solution 2: Another way to solve this problem would be to list all the possibilities in a table:| hamburger | sandwich | quiche | fajita | pizza | |
| soup | soup+burger | ||||
| salad | salad+burger | ||||
| bread | etc |
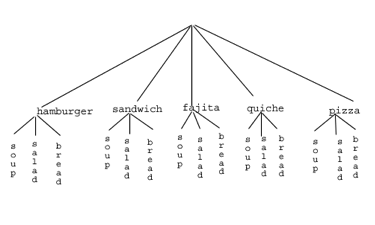 This is called a "tree" diagram because at each stage we branch out, like the branches on a tree. In this case, we first drew five branches (one for each main course) and then for each of those branches we drew three more branches (one for each appetizer). We count the number of branches at the final level and get (surprise, surprise!) 15.
If we wanted, we could instead draw three branches at the first stage for the three appetizers and then five branches (one for each main course) branching out of each of those three branches.
This is called a "tree" diagram because at each stage we branch out, like the branches on a tree. In this case, we first drew five branches (one for each main course) and then for each of those branches we drew three more branches (one for each appetizer). We count the number of branches at the final level and get (surprise, surprise!) 15.
If we wanted, we could instead draw three branches at the first stage for the three appetizers and then five branches (one for each main course) branching out of each of those three branches.
Basic Counting Rule
If we are asked to choose one item from each of two separate categories where there are m items in the first category and n items in the second category, then the total number of available choices is m · n. This is sometimes called the multiplication rule for probabilities.examples
Example 1: There are 21 novels and 18 volumes of poetry on a reading list for a college English course. How many different ways can a student select one novel and one volume of poetry to read during the quarter?Answer: There are 21 choices from the first category and 18 for the second, so there are 21 · 18 = 378 possibilities.
The Basic Counting Rule can be extended when there are more than two categories by applying it repeatedly, as we see in the next example. Example 2: Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks), five choices for a main course (hamburger, sandwich, quiche, fajita or pasta) and two choices for dessert (pie or ice cream). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?Answer: There are 3 choices for an appetizer, 5 for the main course and 2 for dessert, so there are 3 · 5 · 2 = 30 possibilities.
Example 3: A quiz consists of 3 true-or-false questions. In how many ways can a student answer the quiz?Answer: There are 3 questions. Each question has 2 possible answers (true or false), so the quiz may be answered in 2 · 2 · 2 = 8 different ways. Recall that another way to write 2 · 2 · 2 is 23, which is much more compact.
These basic counting examples are described in the following video. https://youtu.be/fROqcu-ekkwTry It
[ohm_question]7159[/ohm_question]Permutations
Next, we will develop an even faster way to solve some of the problems we have already learned to solve by other means. Let's start with an example.example
How many different ways can the letters of the word MATH be rearranged to form a four-letter code word?Answer: This problem is a bit different. Instead of choosing one item from each of several different categories, we are repeatedly choosing items from the same category (the category is: the letters of the word MATH) and each time we choose an item we do not replace it, so there is one fewer choice at the next stage: we have 4 choices for the first letter (say we choose A), then 3 choices for the second (M, T and H; say we choose H), then 2 choices for the next letter (M and T; say we choose M) and only one choice at the last stage (T). Thus there are 4 · 3 · 2 · 1 = 24 ways to spell a code with with the letters MATH.
Factorial
For a whole number n, the notation n! (read “n factorial”) is defined as: .Try It
[ohm_question]7188[/ohm_question]example
How many ways can five different door prizes be distributed among five people?Answer: There are 5 choices of people to get the first door prize, 4 choices for the second, and so on. The number of ways the prizes can be distributed will be 5! = 5 · 4 · 3 · 2 · 1 = 120 ways.
Try It
[ohm_question]7191[/ohm_question]Permutations
We define the notation as follows:
We say that there are permutations of size r that may be selected from among n choices without replacement when order matters. It turns out that we can express this result more simply using factorials.
Examples
Example 1: I have nine paintings and have room to display only four of them at a time on my wall. How many different ways could I do this?Answer: Since we are choosing 4 paintings out of 9 without replacement where the order of selection is important there are 9P4 = 9 · 8 · 7 · 6 = 3,024 permutations.
Example 2: How many ways can a four-person executive committee (president, vice-president, secretary, treasurer) be selected from a 16-member board of directors of a non-profit organization?Answer: We want to choose 4 people out of 16 without replacement and where the order of selection is important. So the answer is 16P4 = 16 · 15 · 14 · 13 = 43,680.
View this video to see more about the permutations examples. https://youtu.be/xlyX2UJMJQITry It
[ohm_question]7193[/ohm_question]Combinations
In the previous section we considered the situation where we chose r items out of n possibilities without replacement and where the order of selection was important. We now consider a similar situation in which the order of selection is not important.Combinations
We define the notation as follows: .
We say that there are combinations of size r that may be selected from among n choices without replacement where order doesn’t matter.
Example
A group of four students is to be chosen from a 35-member class to represent the class on the student council. How many ways can this be done?Answer: Since we are choosing 4 people out of 35 without replacement where the order of selection is not important there are = 52,360 combinations.
Example
The United States Senate Appropriations Committee consists of 29 members, 15 Republicans and 14 Democrats. The Defense Subcommittee consists of 19 members, 10 Republicans and 9 Democrats. How many different ways can the members of the Defense Subcommittee be chosen from among the 29 Senators on the Appropriations Committee?Answer: In this case we need to choose 10 of the 15 Republicans and 9 of the 14 Democrats. There are 15C10 = 3003 ways to choose the 10 Republicans and 14C9 = 2002 ways to choose the 9 Democrats. But now what? How do we finish the problem? Suppose we listed all of the possible 10-member Republican groups on 3003 slips of red paper and all of the possible 9-member Democratic groups on 2002 slips of blue paper. How many ways can we choose one red slip and one blue slip? This is a job for the Basic Counting Rule! We are simply making one choice from the first category and one choice from the second category, just like in the restaurant menu problems from earlier. There must be 3003 · 2002 = 6,012,006 possible ways of selecting the members of the Defense Subcommittee.
This example is worked through below. https://youtu.be/Xqc2sdYN7xo